Binary Tree Maximum Path Sum Problem

Problem Description
Level: medium
Given a binary tree, find the maximum path sum. The path may start and end at any node in the tree.

Example
Given the below binary tree:


  1
 / \
2   3

/ \

2 3

return 6

Analysis:

1. Consider divide and conquer algorithm
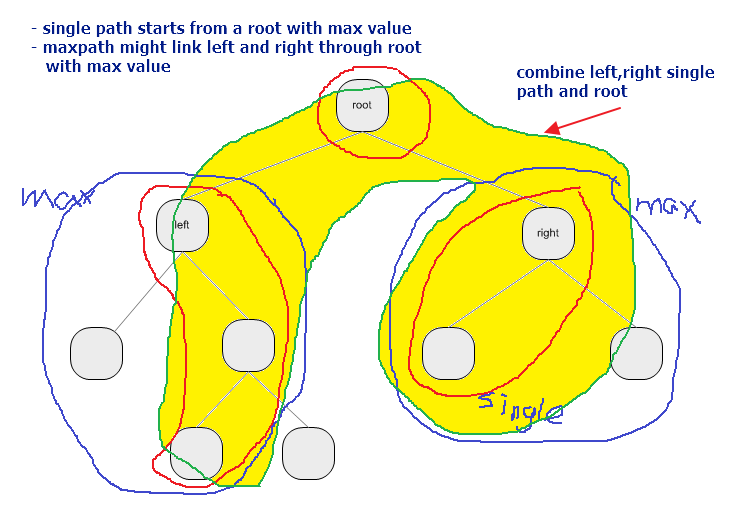
2. for any root, left and right side will have a max path [from a node (may be root / child node)], to a linked node [may be root / child node)], also include a single path (from root to a child node, then next child node etc)
3. pick up the maximum value of the max path (left and right), assume the result is V1
4. calculate the left single path + right single path + root value (will be a potential max path), assume the result is V2
5. compare V1 and V2, and choose the max value in V1 and V2 as the new the max path value.

Solution:


    public int maxPathSum(TreeNode root) {
    	return helper(root).maxPath;
    }
    
    private ResultType helper(TreeNode root) {
    	if(root == null) {
    		return new ResultType(0, Integer.MIN_VALUE);
    	}
    	
    	// divide
    	ResultType left = helper(root.left);
    	ResultType right = helper(root.right);
    	
    	// conquer
    	int singlePath = Math.max(left.singlePath, right.singlePath) + root.val;
    	singlePath = Math.max(singlePath, 0);
    	
    	int maxPath = Math.max(left.maxPath, right.maxPath);
    	maxPath = Math.max(maxPath, left.singlePath + right.singlePath + root.val);
    	
    	return new ResultType(singlePath, maxPath);
    }
    
    private class ResultType {
    	int singlePath;
    	int maxPath;
    	
    	ResultType(int singlePath, int maxPath) {
    		this.singlePath = singlePath;
    		this.maxPath = maxPath;
    	}
    }