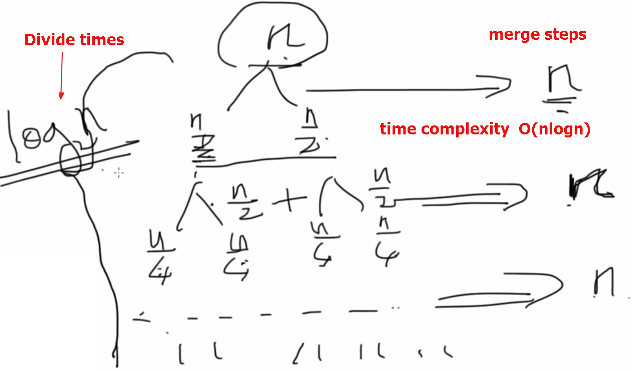
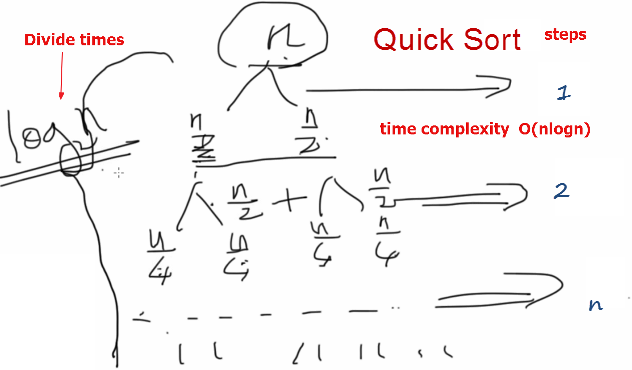
The merge sort is a recursive sort of order n*log(n).
It is notable for having a worst case and average complexity of O(n*log(n)), and a best case complexity of O(n) (for pre-sorted input). The basic idea is to split the collection into smaller groups by halving it until the groups only have one element or no elements (which are both entirely sorted groups). Then merge the groups back together so that their elements are in order. This is how the algorithm gets its “divide and conquer” description.
Conceptually, a merge sort works as follows Divide & Conquer:
1. Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
2. Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
(from WiKi)
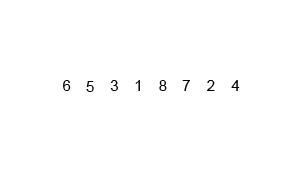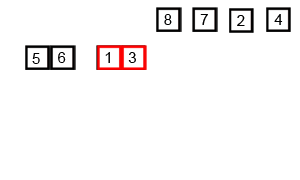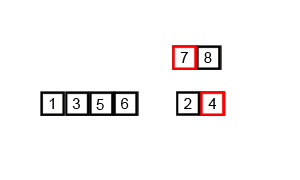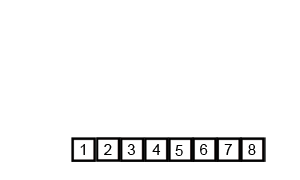
Merge Sort Reference code from web:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import java.util.List; import java.util.ArrayList; import java.util.Iterator; public class Merge{ public static <E extends Comparable<? super E>> List<E> mergeSort(List<E> m){ if(m.size() <= 1) return m; int middle = m.size() / 2; List<E> left = m.subList(0, middle); List<E> right = m.subList(middle, m.size()); right = mergeSort(right); left = mergeSort(left); List<E> result = merge(left, right); return result; } public static <E extends Comparable<? super E>> List<E> merge(List<E> left, List<E> right){ List<E> result = new ArrayList<E>(); Iterator<E> it1 = left.iterator(); Iterator<E> it2 = right.iterator(); E x = it1.next(); E y = it2.next(); while (true){ //change the direction of this comparison to change the direction of the sort if(x.compareTo(y) <= 0){ result.add(x); if(it1.hasNext()){ x = it1.next(); }else{ result.add(y); while(it2.hasNext()){ result.add(it2.next()); } break; } }else{ result.add(y); if(it2.hasNext()){ y = it2.next(); }else{ result.add(x); while (it1.hasNext()){ result.add(it1.next()); } break; } } } return result; } } |